【论文解析】多目标多任务优化——将邻域作为知识迁移的桥梁
| Title | Multiobjective Multitask Optimization-Neighborhood as a Bridge for Knowledge Transfering |
|---|---|
| Author | Xianpeng Wang; Zhiming Dong; Lixin Tang; Qingfu Zhang |
| Affiliations | Northeastern University |
| Emails | wangxianpeng@ise.neu.edu.cn |
| Paper | https://ieeexplore.ieee.org/document/9721409/ |
论文摘要
本文提出了一种基于分解的多目标多任务优化算法,缩写为MTEA/D-DN。该算法使用两种不同的邻域关系来实现任务之间的知识转移。多目标多任务优化问题是指在一个优化问题中同时考虑多个目标和多个任务的问题。本文中,作者使用MOEA/D框架将每个任务分解为多个单目标子问题,然后使用邻域结构实现不同子问题之间的协作。邻域结构是指相邻的子问题之间具有相似的最优解,传统多目标优化中MOEA/D利用这种邻域关系在不同子问题之间进行知识转移,而本文使用两种不同的邻域关系来实现任务之间的知识转移,即内部邻域和外部邻域。内部邻域是指在同一任务中的相邻子问题之间的邻域关系,而外部邻域是指不同任务之间的相邻子问题之间的邻域关系。作者在多个基准测试实例和钢铁厂的一个实际多目标多任务优化问题上进行了实验,结果表明,该算法在这些问题上表现出更具竞争力的结果。
问题导入
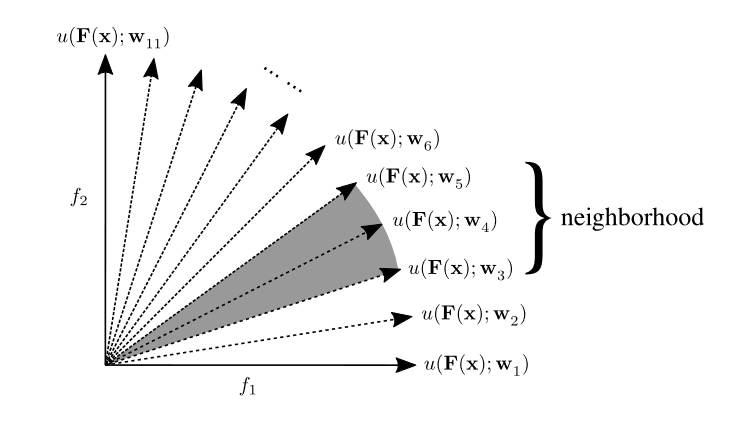
neighborhood example
MOEA/D 中的邻域定义了多目标优化中不同子问题之间的关系。它假设相邻子问题具有相似的最优解 ,而相邻子问题的优化过程之间的协作可以看作是同一任务内部的局部知识挖掘。这样的思路在多任务优化中同样有着拓展意义,在本文中,首先采用 MOEA/D 框架将每个单独的任务分解为多个单目标子问题,随后在优化过程中探索了来自不同任务的子问题的邻域之间的关系。这样就实现了不同任务之间的知识共享和交换。本文提出的算法可以总结为基于双邻域分解的 MO-MTO EA,也就是Multiobjective multiTask optimization EA based on Decomposition with Dual Neighborhoods (MTEA/D-DN),为了适应多任务优化问题的特性,算法中将使用两种不同的邻域关系来实现任务间的知识迁移。
算法流程
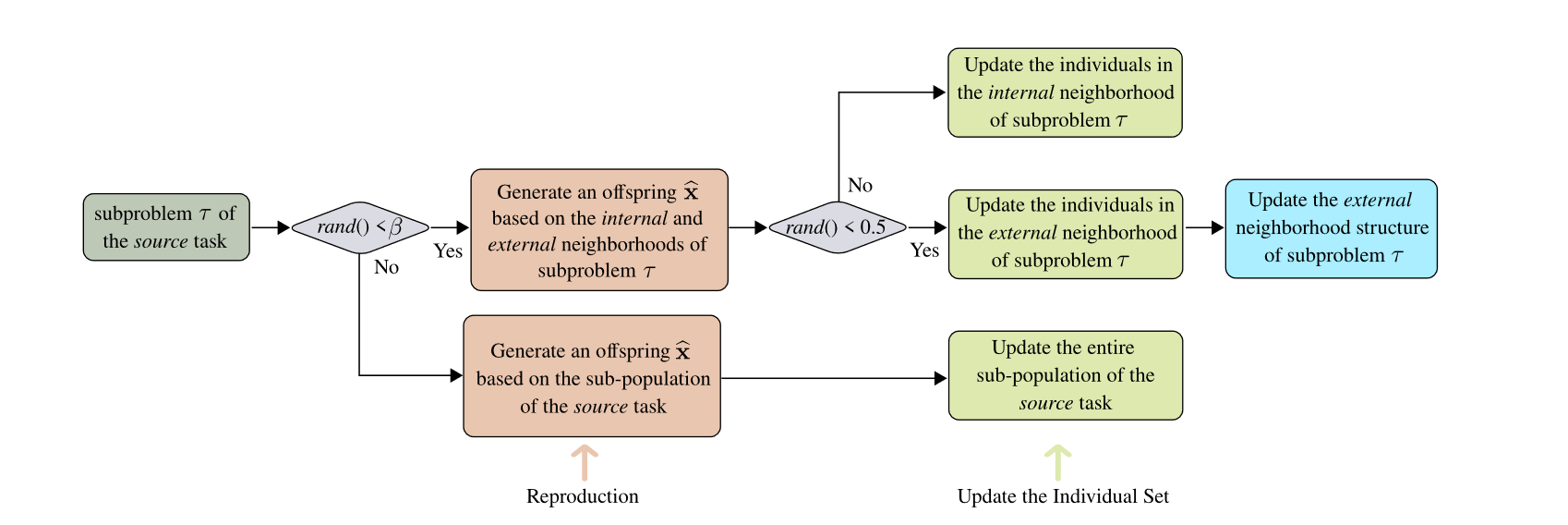
flowchart
对整个算法进行总结后,可以得到其基本流程如下:
- 初始化种群、当前理想解集、外层邻域结构与内部邻域结构。
- 为每个任务k中的子问题根据一定的概率选择使用邻域中的种群作为父代来产生新的子种群或是直接产生子种群。
- 以50%的概率分别使用内部邻域与外部邻域的种群作为父代生成后代个体,如果使用了外部邻域则更新外部邻域结构。
- 重复上述繁殖与更新个体的步骤直至达到收敛标准。
- 输出最优种群。
算法细节
接下来,我们将分别进一步阐述算法中的每个部分。
初始化
对于MTEA/D-DN来说,需要进行初始化的变量较多,其中比较重要的是每个任务中子问题的内部邻域结构与外部邻域结构。在确定邻域的大小之后,内部邻域的确定较为简单,经过MOEA/D算法的分解之后,每个子问题可以表示为一个具体的向量,因此子问题间是否相邻可以通过简单计算两个子问题之间的欧式距离进行判断,随后在内部邻域的初始化过程中选择距离最小的子问题集即可。而外部邻域由于缺乏直接评估的手段与指标,随机选取属于其他任务中的子问题的邻域即可作为其初始值。
需要注意的是,尽管在多任务优化问题中,不同任务的种群被映射到一个统一搜索空间里,但是当我们需要对种群中的个体进行评估时,仍然需要将其先映射到原始的搜索空间中。
繁殖过程
繁殖过程对应了算法中的主循环过程。在这一过程里,在每次循环中,将一个任务包含的具体子问题作为源任务,根据一个确定的概率,随机选择使用内部与外部邻域作为父代种群或是使用当前任务的子种群作为父代种群。在确定父代的候选集后,在确定使用邻域知识进行协助进化的候选集中,以50%的概率选择内部邻域或外部邻域作为产出后代的知识源,并进行后面所述的个体集更新过程与外部邻域更新过程。在繁殖过程中,本算法使用了差分进化中的DE交叉算子与多项式突变运算符获得后代。
个体集的更新过程
首先要确定个体集Q来自哪一任务,也就是知识迁移过程中种群待更新的目标任务,然后使用目标任务对新产生的后代个体进行评估,并在这一过程之后更新当前理想值。本文使用ASF函数来指导完成这一更新过程:
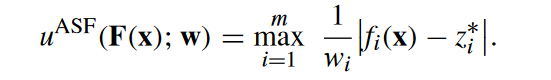
Alt text
这一公式的实质是计算一个加权平均值的最大值,其中每个元素都被其在权重向量中的权重除以,并计算其与达到其参考值的最大距离,这个最大值代表了所有参考值下的最差情况。
当基于子问题的邻域生成后代时,算法中需要决定它应该替换哪个邻域的当前解决方案。本文中选择以0.5的概率随机更新子问题的内部邻域或外部邻域,期望这样能够使得任务之间的信息交换既充分又高效。
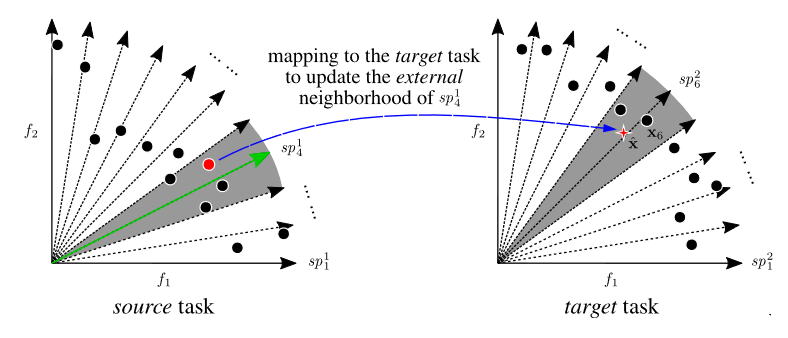
updating external
更新外部邻域的图示。绿色箭头表示源任务中当前优化的子问题 sp14 的权重向量,红色实心圆圈表示基于该子问题生成的后代,然后映射到目标任务,由红色实心星号(表示为 $\hat{x}$)表示。很明显,$\hat{x}$比 x6 具有更有利的位置,因此,源任务能够帮助目标任务。
外部邻域结构的更新过程
我们用$\Lambda$记录外部邻域内其解已被后代$\hat{x}$ 更新的子问题,如果集合为空,则证明目前优化的子问题无法更新其外部邻域内的任何子问题,那么重置优化子问题的外部邻域。否则,使用灰色关联度分析方法来选择具有最大灰色关系等级的集合中子问题的内部邻域,并将其作为优化子问题的外部邻域。
实验结果
Benchmark
result1
result2
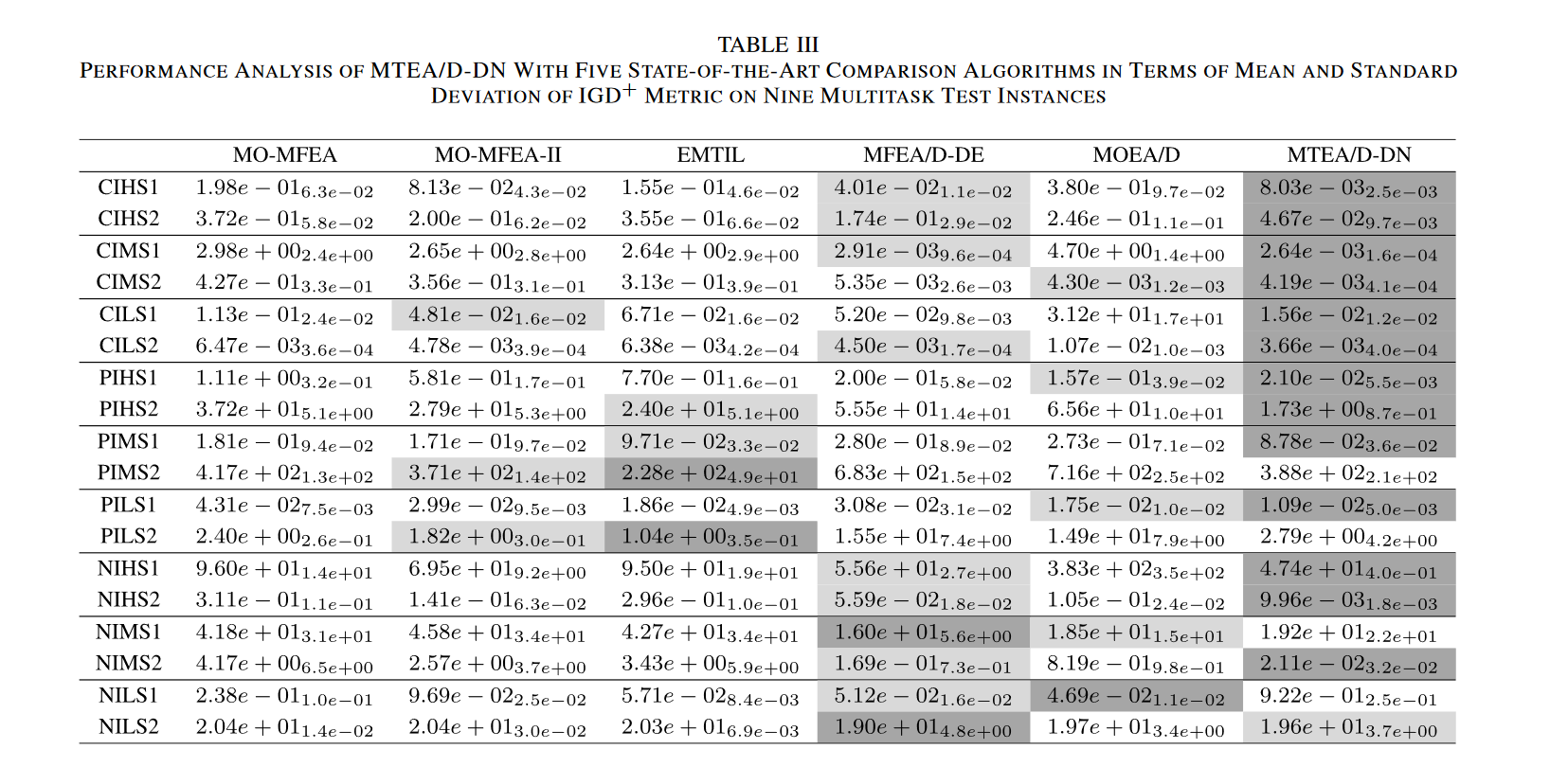
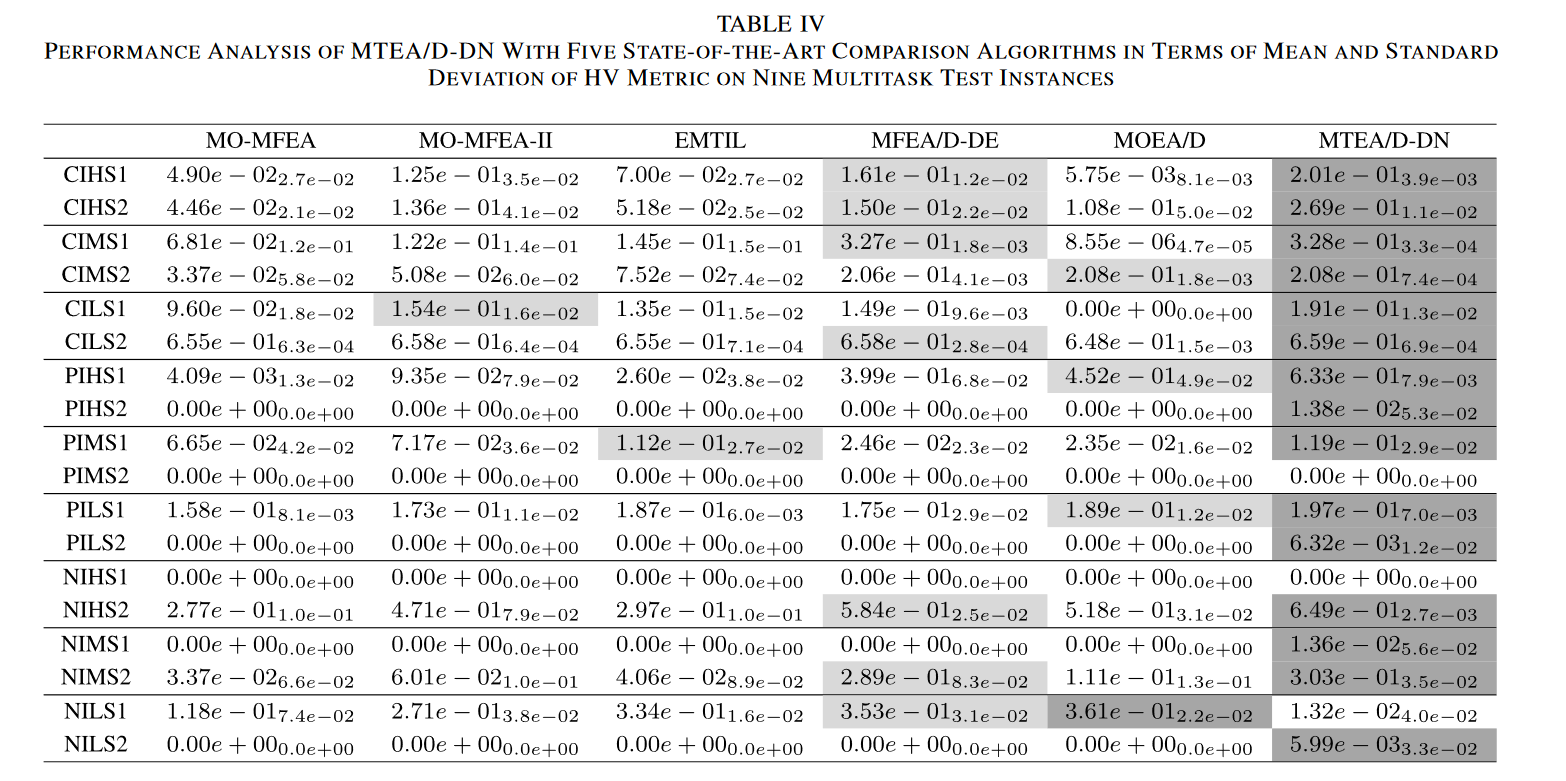
与多任务/多任务测试实例上最先进的算法的比较:表 III 和表 IV 分别显示了我们提出的算法及其竞争对手算法在九个多任务测试实例上关于 IGD+ 和 HV 指标的均值和标准偏差的统计分析结果。实现最佳性能的算法用深灰色阴影标记,实现第二好的算法用浅灰色阴影标记。总的来说,很明显,对于IGD+和HV指标,统计结果表明我们提出的算法比其竞争对手算法表现更好。
具体来说,在这九个测试实例中,我们提出的算法在IGD+和HV指标方面获得了13个和15个单独任务的最佳结果。由于没有算法可以获得主导参考点的解,因此PIMS2和NIHS1的HV指标在表IV中均为0。同样基于分解策略的多任务 EA MFEA/D-DE 表现第二好,浅灰色阴影覆盖率最高。表明基于分解的多目标EA适用于解决MO-MTO问题。表V显示了我们提出的算法和这些最先进的算法在IGD+和HV指标的Wilcoxon秩和检验上的统计分析结果。从这个表中可以清楚地看出,我们提出的算法在大多数测试问题上明显优于这些最先进的算法。
微观洞察中的知识迁移机制
distribution
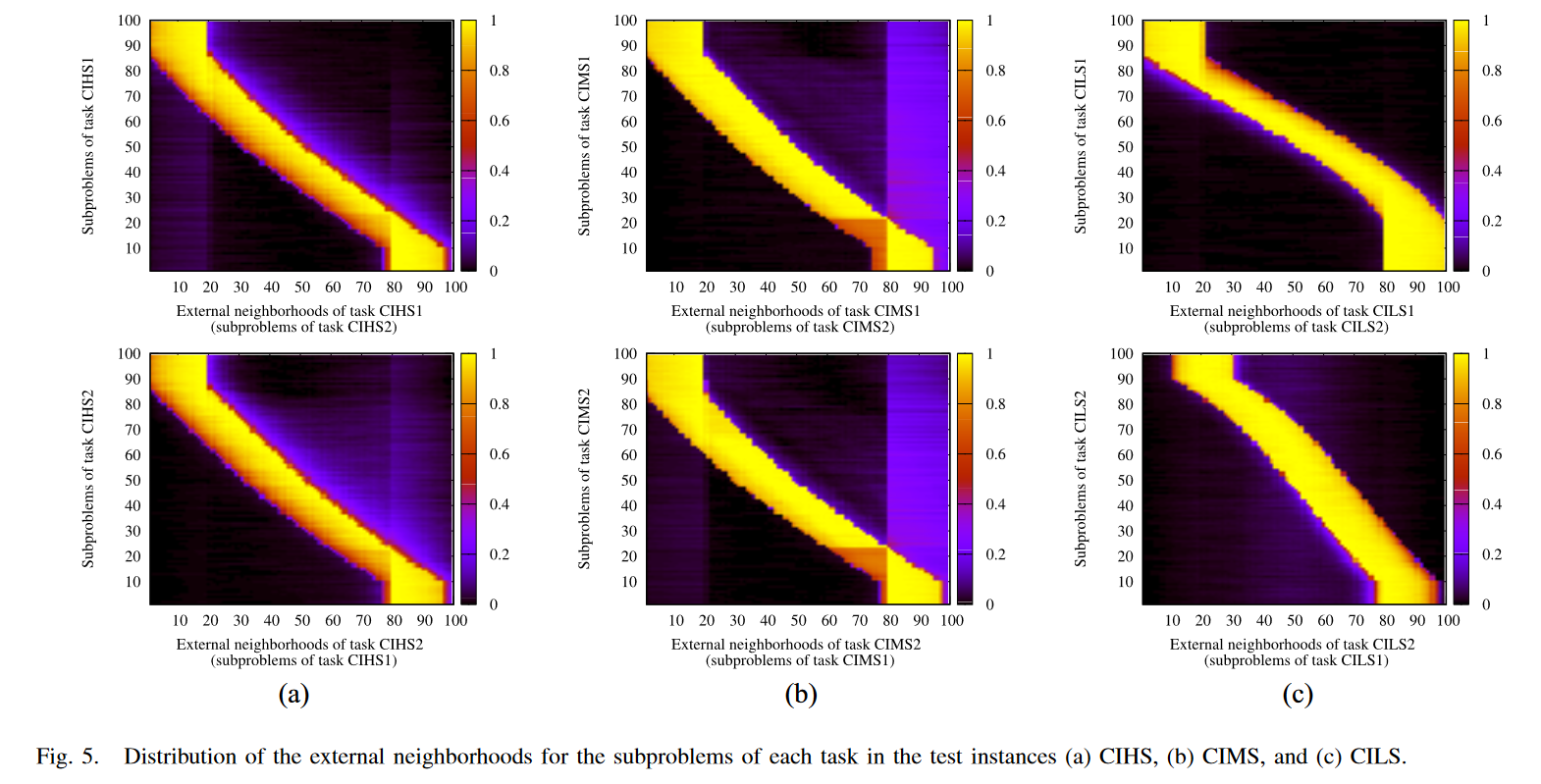
图5显示了测试实例CIHS、CIMS和CILS中每个任务的子问题的外部邻域分布。显然,这三个测试实例中每个任务的子问题的外部邻域具有相似的分布。以CIHS为例,如图5(a)所示,任务CIHS1中的子问题与任务CIHS2中的子问题表现出几乎线性的关系,任务CIHS2子问题的外部邻域具有相似的分布。也就是说,对于这三个测试实例,其他任务中每个子问题的有价值信息的分布不是任意的。由于我们提出的算法基于分解策略,它使邻域充当不同任务之间的桥梁来挖掘和探索这些有价值的信息,即知识,然后这些知识可以用来提高解决每个任务的效率
Real-World Application
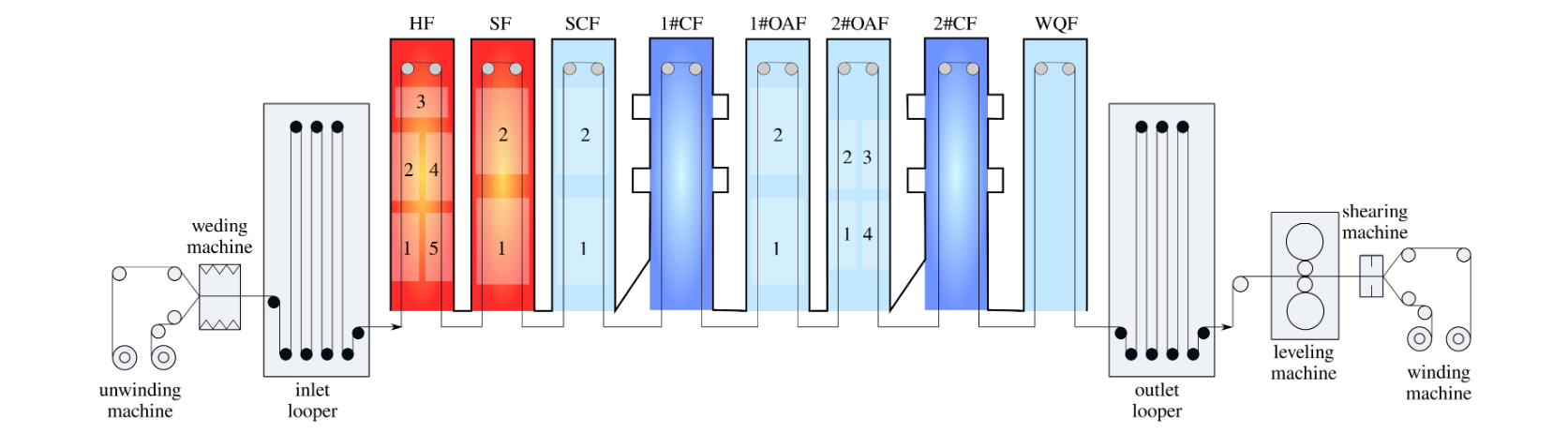
连续退火是钢铁企业冷轧厂的重要生产工艺,其能耗和生产成本通常占整个冷轧厂的较高比例。如下图所示,连续退火线通过将前一带的尾部焊接到下一条钢带的头部来进行不间断生产。焊接钢带依次通过加热炉 (HF), 均热炉 (SF), 慢冷炉 (SCF), 第一冷却炉 (1#CF), 第一过时效炉 (1#OAF), 第二过时效炉 (2#OAF), 第二冷却炉 (2#CF), 水淬炉 (WQF), 校平机, 和机组内的其他区域.每个区域都包含多个工艺操作参数,因此整个生产线有数十个参数。对于每条钢带,其运行设置是一个三目标优化问题,即最大限度地提高产品质量、最大化单位容量和最小化能耗。尽管尺寸和性能不同, 钢带都处于相同的生产环境中.因此,多钢带加工操作参数的最佳设置是一个MO-MTO问题。
从下面的两个表中可以看出,基于分解的多任务 EA、MFEA/D-DE 和我们提出的算法 MTEA/D 在 IGD+ 指标和 HV 指标方面的性能都优于其他算法。此外,我们提出的算法通过使用基于两个邻域的更有针对性的知识挖掘策略来获得最佳性能指标。
continuous annealing

result3
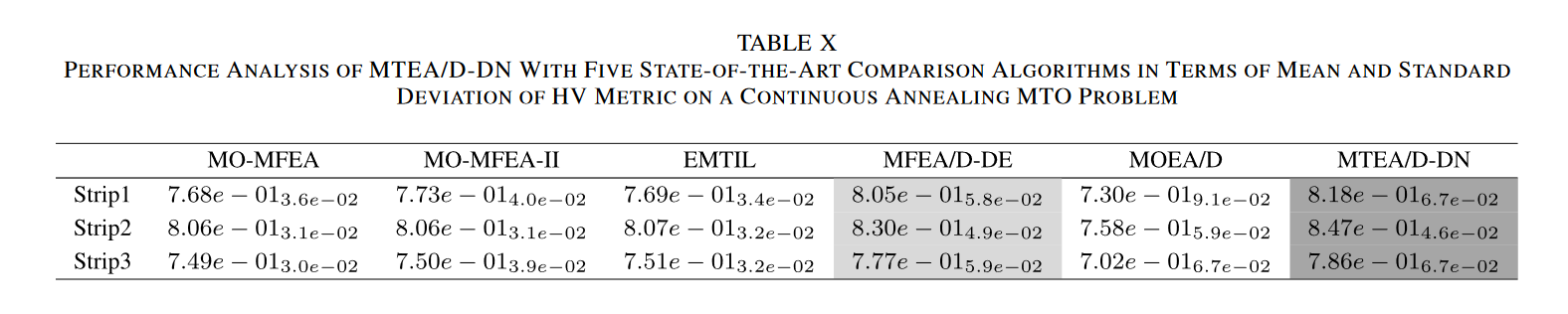
result4
总结与反思
通过构建内部邻域与外部邻域的双层结构,MTEA/D-DN成功构建了任务间知识迁移的桥梁,探索了不同任务之间的相关性,使得任务之间可以进行有针对性的信息交换。然而,这一算法仍然没有回答知识迁移中最令人瞩目的负迁移现象应该如何解决,以及邻域大小对算法性能带来的巨大影响使得这一算法的性能并不鲁棒。基于这些不足,我姑且认为可以尝试从以下几个角度对算法进行进一步的优化:
- 引入动态邻域调整机制,例如邻域大小线性缩减方法等。
- 对于邻域这一概念来说,更大规模的优化任务集本身可能带来的性能提升更加显著,但是对于评估其外部邻域的方法来说,灰色关联度分析可能有所不足,并且在初始化时采用的随机策略也可能导致后续优化的效果较差。