【论文分享】Generative Time-Series Modeling With Fourier Flows
| Title | Generative Time-Series Modeling With Fourier Flows |
|---|---|
| Author | Ahmed M. Alaa; Alex J. Chan; Mihaela van der Schaar |
| Affiliations | University of California, Los Angeles, USA University of Cambridge, UK |
| Emails | ahmedmalaa@ucla.edu |
| Paper | https://paperswithcode.com/paper/generative-time-series-modeling-with-fourier |
| Code | https://github.com/ahmedmalaa/Fourier-flows |
Abstract
Generating synthetic time-series data is crucial in various application domains, such as medical prognosis, wherein research is hamstrung by the lack of access to data due to concerns over privacy. Most of the recently proposed methods for generating synthetic time-series rely on implicit likelihood modeling using generative adversarial networks (GANs)—but such models can be difficult to train, and may jeopardize privacy by “memorizing” temporal patterns in training data. In this paper, we propose an explicit likelihood model based on a novel class of normalizing flows that view time-series data in the frequency-domain rather than the time-domain. The proposed flow, dubbed a Fourier flow, uses a discrete Fourier transform (DFT) to convert variable-length time-series with arbitrary sampling periods into fixed length spectral representations, then applies a (data-dependent) spectral filter to the frequency-transformed time-series. We show that, by virtue of the DFT analytic properties, the Jacobian determinants and inverse mapping for the Fourier flow can be computed efficiently in linearithmic time, without imposing explicit structural constraints as in existing flows such as NICE (Dinh et al. (2014)), RealNVP (Dinh et al. (2016)) and GLOW (Kingma & Dhariwal (2018)). Experiments show that Fourier flows perform competitively compared to state-of-the-art baselines.
1.Introduction
在数据共享可能导致隐私泄露的应用领域,缺乏对数据的访问是开发机器学习解决方案的主要障碍。在本文中,我们专注于时间序列数据设置,其中在任意时间段内以不同特征的不同观测频率顺序收集观测值。在数据共享可能导致隐私泄露的应用领域,缺乏对数据的访问是开发机器学习解决方案的主要障碍。在本文中,我们专注于时间序列数据设置,其中在任意时间段内以不同特征的不同观测频率顺序收集观测值。这些模型通过递归神经网络(RNN)与对抗性训练相结合来应用表示学习,以便将潜在空间中的噪声序列映射到输出空间中的合成序列数据。尽管能够灵活地学习复杂的表示,但基于GAN的模型可能很难训练(Srivastava et al.(2017)),尤其是在复杂的时间序列数据设置中。此外,由于它们依赖于隐式似然建模,由于缺乏明确可计算的似然函数,基于GAN的模型可能很难定量评估。最后,GANs很容易受到训练数据记忆的影响(Nagarajan et al.(2018)),这一问题在时间环境中会加剧,因为只记忆医疗时间序列的一部分可能足以揭示患者的身份,这首先违背了使用合成数据的初衷。在这里,我们提出了一种基于一类新的归一化流(我们称之为傅立叶流)生成时间序列数据的替代显式似然方法。我们提出的基于流量的模型在频域而不是时域中对时间序列数据进行操作,它使用离散傅立叶变换(DFT)将不同特征之间具有不同采样率的可变长度时间序列转换为固定大小的频谱表示,然后通过将数据相关的频谱滤波器链应用于频率变换的时间序列来学习数据在频域中的分布。
2.Preliminaries
傅立叶变换是一种数学运算,可将有限长度、定期采样的时域信号 x 转换为其频域表示形式 X 。 T 点离散傅里叶变换 (DFT),表示为 X = FT {x},变换一个(复值)时间戳序列 x , {x0, . . . , xT −1} 转换成长度为 T 的(复值)频率分量序列 X , {X0, . . . , XT -1}, 通过以下操作:
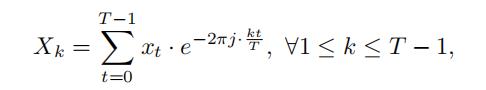
formular1
因此,傅里叶变换将任何时间序列分解为不同频率的正弦信号的线性组合——由此产生的频率分量序列 X 对应于分配给构成时域信号 x 的正弦信号的不同频率的系数。在涉及数字信号处理和通信的许多实际应用中,DFT 是一个关键的计算和概念工具 。
3.傅里叶流
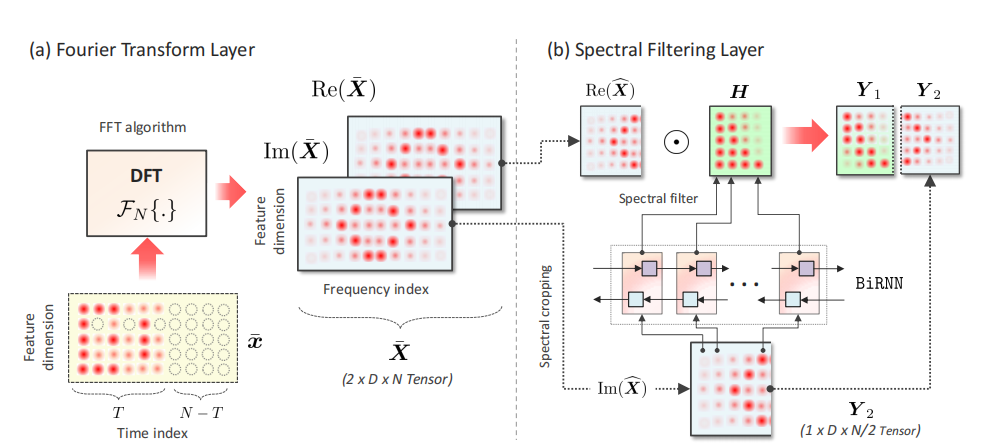
我们提出了一种新的时间序列数据流,即傅里叶流,简而言之,傅立叶流包括两个步骤:(a) 频率变换层,然后是 (b) 数据相关的光谱过滤层。下表和下图总结了傅里叶流中涉及的步骤。
structure

table
3.1 Frequency Transform Layer
在建议流程的第一步中,我们转换时间序列 x = [ x0, . . . , xT -1 ] 通过傅里叶变换转换为它的频谱表示——我们通过将 DFT 操作独立地应用于每个特征维度 d 来实现。让 x d = [ x0,d[rd], . . . , xT −1,d[rd] ] 是与特征维度 d 关联的时间序列;傅立叶变换层为所有 d ∈ {1, . . . , D}通过以下三个步骤:
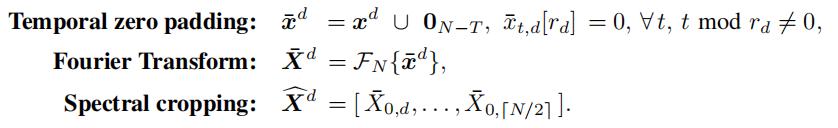
formular2
3.2 Spectral Filtering Layer
傅里叶流的第二层是仿射耦合层,应用于频域中的时间序列 x 如下:(log H, M) = BiRNN(Im(cX)), Y1 = H Re(cX) + M, Y2 = Im(Xc), Y = concat(Y1,Y2),其中H和µ为D×N矩阵,BiRNN表示a双向递归神经网络 (Schuster & Paliwal (1997)),表示 Hadamard(逐元素)积。在这里,我们在 Xc 中拆分实部和虚部通道。 频域中的仿射变换可以被认为是一种频谱滤波操作,其中时间序列的偶数部分 Re(bX) 的频率变换应用于具有传递函数 H 的滤波器。传递函数本身是数据相关的:它取决于 Im(bX),或者等效地,时间序列 x 的奇数部分的频率变换形式。从 Im(bX) 到传递函数 H 的映射是通过一个 RNN 实现的,该 RNN 在所有不同的频率分量之间共享参数,因为对于具有大 T 的时间序列,N 可以变得非常大。我们使用双向 RNN,因为所有我们同时可以使用频率组件。
3.3 时域中的傅里叶流
傅立叶流映射在时域中看起来如何?利用 DFT 的卷积特性(第 3.2 节),傅里叶流的时域视图可以表示如下
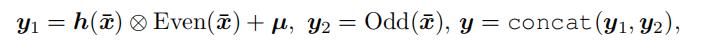
formular3
傅里叶流的时域视图阐明了其多方面的建模优势。首先,与现有方法的耦合层中的逐元素仿射变换相比,在 (8) 中具有更具表现力的卷积变换具有代表性优势。此外,傅里叶流不需要不连续地拆分特征维度,而是将每个特征分解为其偶数和奇数分量。其次,这种更丰富的表示没有额外的计算成本:虽然时域卷积将在 O(N2D2) 时间内运行,但我们的光谱滤波器在频域,DFT 在 O(DN log N) 时间内运行。雅可比行列式的计算是通过简单地添加 H 的所有元素来实现的,就像时域仿射耦合方法中的情况一样。最后,DFT 操作可以处理可变长度的时间序列和跨特征的不一致采样周期,而无需任何额外的建模工作。
Discussion
在本文中,我们介绍了一种基于一类新型归一化流的显式似然模型,该模型对频域而非时域中随机时间序列数据的分布进行建模。利用傅里叶变换的特性,所提出的流程自然地处理任意采样率和时间序列数据的持续时间,并且与现有方法相比能够学习更丰富的表示,而无需额外的计算成本。傅立叶流具有三个建模优势,使它们能够准确地对时间序列分布进行建模。首先,DFT 层将时间信息压缩为低维频谱表示,从而实现更高效的分布学习。例如,考虑第 5.1 节中的正弦示例。在此示例中,数据取自随机过程 sin(f t + φ),其中 f 是随机频率。要使用传统方法对从此类过程中提取的长度 T 时间序列进行建模,我们需要对 T 维随机变量进行建模。然而,使用 DFT 变换,我们将对光谱表示 X = 2 / j [δ(v + f) − δ(v − f)] 建模,其中 δ 是 Dirac-delta 函数。因此,可以用一条信息完全描述频谱表示,该信息是频率分量 f 的位置,即一维随机变量。其次,傅里叶流可以构建复杂的变换,而无需为 Jacobean 计算增加额外成本。也就是说,一个 DFT 层后跟一个简单的变换(例如仿射变换)将相当于一个复杂的整体变换,而没有任何与 Jacobean 变换相关的额外复杂性。最后,在新型光谱过滤层中使用 RNN 模型可捕获光谱数据的顺序性质。